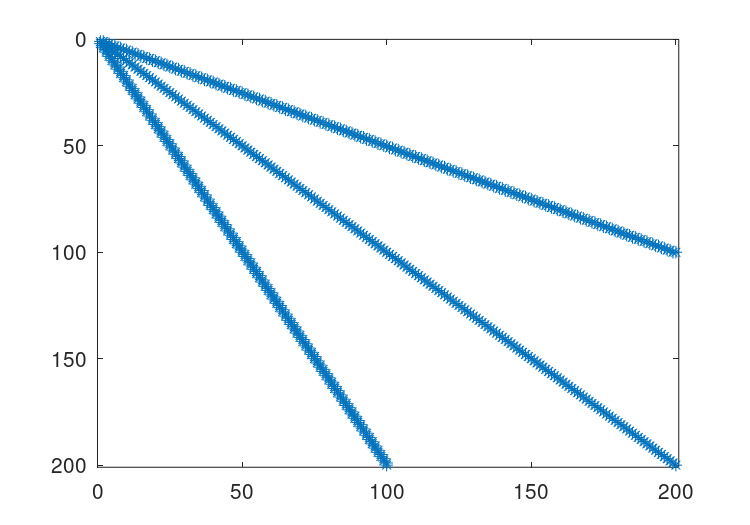
Figure 22.1: Structure of simple sparse matrix.
Next: Operators and Functions, Previous: Creating Sparse Matrices, Up: Basics [Contents][Index]
There are a number of functions that allow information concerning sparse matrices to be obtained. The most basic of these is issparse that identifies whether a particular Octave object is in fact a sparse matrix.
Another very basic function is nnz that returns the number of nonzero entries there are in a sparse matrix, while the function nzmax returns the amount of storage allocated to the sparse matrix. Note that Octave tends to crop unused memory at the first opportunity for sparse objects. There are some cases of user created sparse objects where the value returned by nzmax will not be the same as nnz, but in general they will give the same result. The function spstats returns some basic statistics on the columns of a sparse matrix including the number of elements, the mean and the variance of each column.
Return true if x is a sparse matrix.
See also: ismatrix.
Return a column vector of the nonzero values of the matrix A.
Return the amount of storage allocated to the sparse matrix SM.
Programming Note: Octave tends to crop unused memory at the first opportunity
for sparse objects. Thus, in general the value of nzmax will be the
same as nnz, except for some cases of user-created sparse objects.
Also, note that Octave always reserves storage for at least one value. Thus,
for empty matrices nnz will report 0, but nzmax will report 1.
Return the stats for the nonzero elements of the sparse matrix S.
count is the number of nonzeros in each column, mean is the mean of the nonzeros in each column, and var is the variance of the nonzeros in each column.
Called with two input arguments, if S is the data and j is the
bin number for the data, compute the stats for each bin. In this case,
bins can contain data values of zero, whereas with
spstats (S) the zeros may disappear.
When solving linear equations involving sparse matrices Octave determines the means to solve the equation based on the type of the matrix (see Sparse Linear Algebra). Octave probes the matrix type when the div (/) or ldiv (\) operator is first used with the matrix and then caches the type. However the matrix_type function can be used to determine the type of the sparse matrix prior to use of the div or ldiv operators. For example,
a = tril (sprandn (1024, 1024, 0.02), -1) ...
+ speye (1024);
matrix_type (a);
ans = Lower
shows that Octave correctly determines the matrix type for lower triangular matrices. matrix_type can also be used to force the type of a matrix to be a particular type. For example:
a = matrix_type (tril (sprandn (1024, ... 1024, 0.02), -1) + speye (1024), "Lower");
This allows the cost of determining the matrix type to be avoided. However, incorrectly defining the matrix type will result in incorrect results from solutions of linear equations, and so it is entirely the responsibility of the user to correctly identify the matrix type
There are several graphical means of finding out information about sparse matrices. The first is the spy command, which displays the structure of the nonzero elements of the matrix. See Figure 22.1, for an example of the use of spy. More advanced graphical information can be obtained with the treeplot, etreeplot and gplot commands.

Figure 22.1: Structure of simple sparse matrix.
One use of sparse matrices is in graph theory, where the interconnections between nodes are represented as an adjacency matrix. That is, if the i-th node in a graph is connected to the j-th node. Then the ij-th node (and in the case of undirected graphs the ji-th node) of the sparse adjacency matrix is nonzero. If each node is then associated with a set of coordinates, then the gplot command can be used to graphically display the interconnections between nodes.
As a trivial example of the use of gplot consider the example,
A = sparse ([2,6,1,3,2,4,3,5,4,6,1,5],
[1,1,2,2,3,3,4,4,5,5,6,6],1,6,6);
xy = [0,4,8,6,4,2;5,0,5,7,5,7]';
gplot (A,xy)
which creates an adjacency matrix A where node 1 is connected
to nodes 2 and 6, node 2 with nodes 1 and 3, etc. The coordinates of
the nodes are given in the n-by-2 matrix xy.
See Figure 22.2.
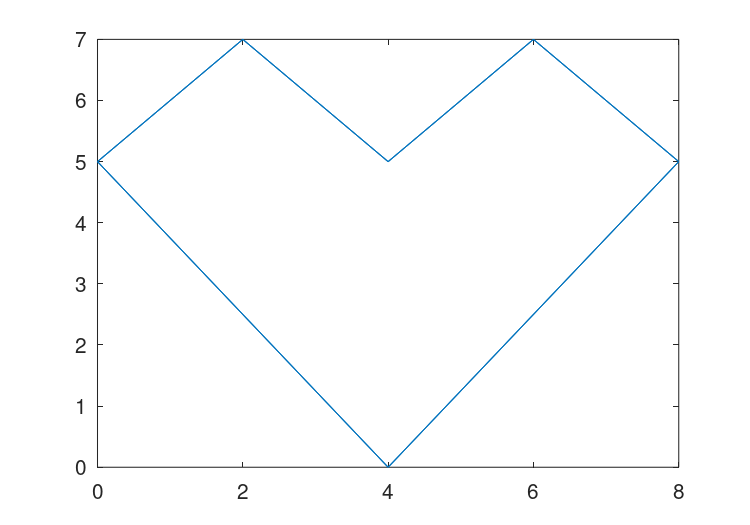
Figure 22.2: Simple use of the gplot command.
The dependencies between the nodes of a Cholesky factorization can be
calculated in linear time without explicitly needing to calculate the
Cholesky factorization by the etree command. This command
returns the elimination tree of the matrix and can be displayed
graphically by the command treeplot (etree (A)) if A is
symmetric or treeplot (etree (A+A')) otherwise.
Plot the sparsity pattern of the sparse matrix x.
If the argument markersize is given as a scalar value, it is used to determine the point size in the plot.
If the string line_spec is given it is passed to plot and
determines the appearance of the plot.
Return the elimination tree for the matrix S.
By default S is assumed to be symmetric and the symmetric elimination
tree is returned. The argument typ controls whether a symmetric or
column elimination tree is returned. Valid values of typ are
"sym" or "col", for symmetric or column elimination tree
respectively.
Called with a second argument, etree also returns the postorder
permutations on the tree.
Plot the elimination tree of the matrix A or
A+A' if A in not symmetric.
The optional parameters node_style and edge_style define the output style.
Plot a graph defined by A and xy in the graph theory sense.
A is the adjacency matrix of the array to be plotted and xy is an n-by-2 matrix containing the coordinates of the nodes of the graph.
The optional parameter line_style defines the output style for the plot. Called with no output arguments the graph is plotted directly. Otherwise, return the coordinates of the plot in x and y.
Produce a graph of tree or forest.
The first argument is vector of predecessors.
The optional parameters node_style and edge_style define the output plot style.
The complexity of the algorithm is O(n) in terms of is time and memory requirements.
treelayout lays out a tree or a forest.
The first argument tree is a vector of predecessors.
The parameter permutation is an optional postorder permutation.
The complexity of the algorithm is O(n) in terms of time and memory requirements.
Next: Operators and Functions, Previous: Creating Sparse Matrices, Up: Basics [Contents][Index]