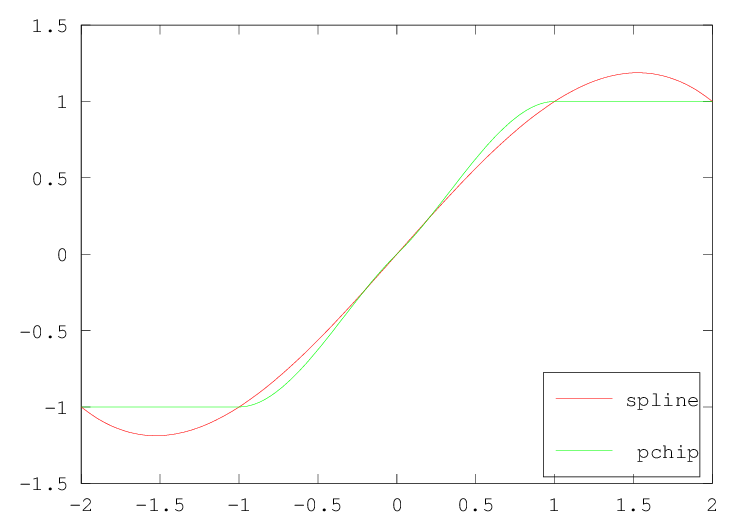
Figure 29.1: Comparison of "pchip" and "spline" interpolation methods for a
step function
Next: Multi-dimensional Interpolation, Up: Interpolation [Contents][Index]
Octave supports several methods for one-dimensional interpolation, most of which are described in this section. Polynomial Interpolation and Interpolation on Scattered Data describe additional methods.
One-dimensional interpolation.
Interpolate input data to determine the value of yi at the points
xi. If not specified, x is taken to be the indices of y
(1:length (y)). If y is a matrix or an N-dimensional
array, the interpolation is performed on each column of y.
The interpolation method is one of:
"nearest"Return the nearest neighbor.
"previous"Return the previous neighbor.
"next"Return the next neighbor.
"linear" (default)Linear interpolation from nearest neighbors.
"pchip"Piecewise cubic Hermite interpolating polynomial—shape-preserving interpolation with smooth first derivative.
"cubic"Cubic interpolation (same as "pchip").
"spline"Cubic spline interpolation—smooth first and second derivatives throughout the curve.
Adding ’*’ to the start of any method above forces interp1
to assume that x is uniformly spaced, and only x(1)
and x(2) are referenced. This is usually faster,
and is never slower. The default method is "linear".
If extrap is the string "extrap", then extrapolate values
beyond the endpoints using the current method. If extrap is a
number, then replace values beyond the endpoints with that number. When
unspecified, extrap defaults to NA.
If the string argument "pp" is specified, then xi should not
be supplied and interp1 returns a piecewise polynomial object. This
object can later be used with ppval to evaluate the interpolation.
There is an equivalence, such that ppval (interp1 (x,
y, method, .
"pp"), xi) == interp1 (x, y,
xi, method, "extrap")
Duplicate points in x specify a discontinuous interpolant. There
may be at most 2 consecutive points with the same value.
If x is increasing, the default discontinuous interpolant is
right-continuous. If x is decreasing, the default discontinuous
interpolant is left-continuous.
The continuity condition of the interpolant may be specified by using
the options "left" or "right" to select a left-continuous
or right-continuous interpolant, respectively.
Discontinuous interpolation is only allowed for "nearest" and
"linear" methods; in all other cases, the x-values must be
unique.
An example of the use of interp1 is
xf = [0:0.05:10];
yf = sin (2*pi*xf/5);
xp = [0:10];
yp = sin (2*pi*xp/5);
lin = interp1 (xp, yp, xf);
near = interp1 (xp, yp, xf, "nearest");
pch = interp1 (xp, yp, xf, "pchip");
spl = interp1 (xp, yp, xf, "spline");
plot (xf,yf,"r", xf,near,"g", xf,lin,"b", xf,pch,"c", xf,spl,"m",
xp,yp,"r*");
legend ("original", "nearest", "linear", "pchip", "spline");
See also: pchip, spline, interpft, interp2, interp3, interpn.
There are some important differences between the various interpolation
methods. The "spline" method enforces that both the first and second
derivatives of the interpolated values have a continuous derivative,
whereas the other methods do not. This means that the results of the
"spline" method are generally smoother. If the function to be
interpolated is in fact smooth, then "spline" will give excellent
results. However, if the function to be evaluated is in some manner
discontinuous, then "pchip" interpolation might give better results.
This can be demonstrated by the code
t = -2:2;
dt = 1;
ti =-2:0.025:2;
dti = 0.025;
y = sign (t);
ys = interp1 (t,y,ti,"spline");
yp = interp1 (t,y,ti,"pchip");
ddys = diff (diff (ys)./dti) ./ dti;
ddyp = diff (diff (yp)./dti) ./ dti;
figure (1);
plot (ti,ys,"r-", ti,yp,"g-");
legend ("spline", "pchip", 4);
figure (2);
plot (ti,ddys,"r+", ti,ddyp,"g*");
legend ("spline", "pchip");
The result of which can be seen in Figure 29.1 and Figure 29.2.
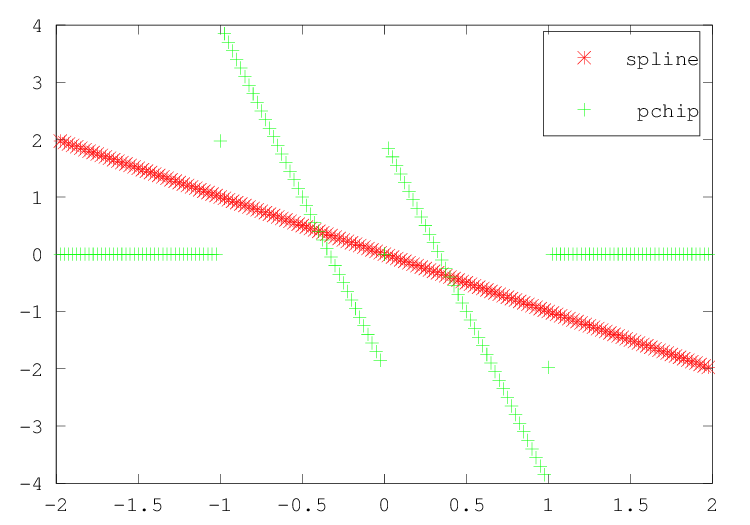
Figure 29.2: Comparison of the second derivative of the "pchip" and "spline"
interpolation methods for a step function
Fourier interpolation, is a resampling technique where a signal is converted to the frequency domain, padded with zeros and then reconverted to the time domain.
Fourier interpolation.
If x is a vector then x is resampled with n points. The data in x is assumed to be equispaced. If x is a matrix or an N-dimensional array, the interpolation is performed on each column of x.
If dim is specified, then interpolate along the dimension dim.
interpft assumes that the interpolated function is periodic, and so
assumptions are made about the endpoints of the interpolation.
See also: interp1.
There are two significant limitations on Fourier interpolation. First,
the function signal is assumed to be periodic, and so non-periodic
signals will be poorly represented at the edges. Second, both the
signal and its interpolation are required to be sampled at equispaced
points. An example of the use of interpft is
t = 0 : 0.3 : pi; dt = t(2)-t(1);
n = length (t); k = 100;
ti = t(1) + [0 : k-1]*dt*n/k;
y = sin (4*t + 0.3) .* cos (3*t - 0.1);
yp = sin (4*ti + 0.3) .* cos (3*ti - 0.1);
plot (ti, yp, "g", ti, interp1 (t, y, ti, "spline"), "b", ...
ti, interpft (y, k), "c", t, y, "r+");
legend ("sin(4t+0.3)cos(3t-0.1)", "spline", "interpft", "data");
which demonstrates the poor behavior of Fourier interpolation for non-periodic functions, as can be seen in Figure 29.3.
In addition, the support functions spline and lookup that
underlie the interp1 function can be called directly.
Return the cubic spline interpolant of points x and y.
When called with two arguments, return the piecewise polynomial pp
that may be used with ppval to evaluate the polynomial at specific
points.
When called with a third input argument, spline evaluates the spline
at the points xi. The third calling form
spline (x, y, xi) is equivalent to
ppval (spline (x, y), xi).
The variable x must be a vector of length n.
y can be either a vector or array. If y is a vector it must
have a length of either n or n + 2. If the length of
y is n, then the "not-a-knot" end condition is used.
If the length of y is n + 2, then the first and last
values of the vector y are the values of the first derivative of the
cubic spline at the endpoints.
If y is an array, then the size of y must have the form
[s1, s2, …, sk, n]
or
[s1, s2, …, sk, n + 2].
The array is reshaped internally to a matrix where the leading
dimension is given by
s1 * s2 * … * sk
and each row of this matrix is then treated separately. Note that this is
exactly the opposite of interp1 but is done for MATLAB
compatibility.
Next: Multi-dimensional Interpolation, Up: Interpolation [Contents][Index]