#include "CmplxHESS.h"#include "dbleHESS.h"#include "fCmplxHESS.h"#include "floatHESS.h"#include "defun-dld.h"#include "error.h"#include "gripes.h"#include "oct-obj.h"#include "utils.h"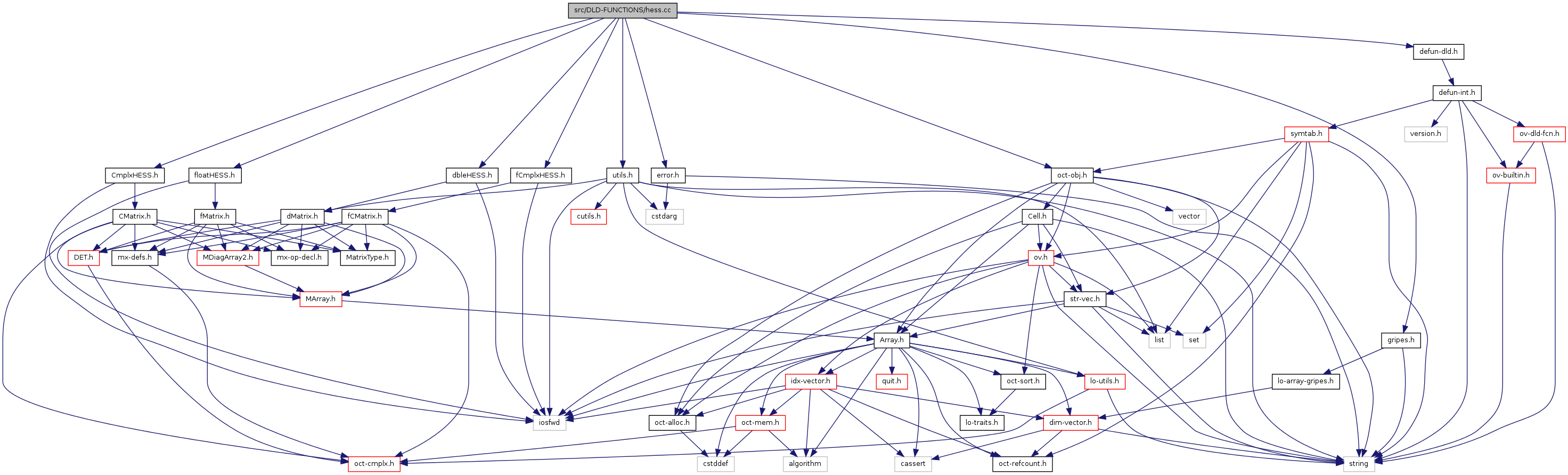
Go to the source code of this file.
Functions | |
| DEFUN_DLD (hess, args, nargout,"-*- texinfo -*-\n\ @deftypefn {Loadable Function} {@var{H} =} hess (@var{A})\n\ @deftypefnx {Loadable Function} {[@var{P}, @var{H}] =} hess (@var{A})\n\ @cindex Hessenberg decomposition\n\ Compute the Hessenberg decomposition of the matrix @var{A}.\n\ \n\ The Hessenberg decomposition is\n\ @tex\n\ $$\n\ A = PHP^T\n\ $$\n\ where $P$ is a square unitary matrix ($P^TP = I$), and $H$\n\ is upper Hessenberg ($H_{i,j} = 0, \\forall i \\ge j+1$).\n\ @end tex\n\ @ifnottex\n\ @code{@var{P} * @var{H} * @var{P}' = @var{A}} where @var{P} is a square\n\ unitary matrix (@code{@var{P}' * @var{P} = I}, using complex-conjugate\n\ transposition) and @var{H} is upper Hessenberg\n\ (@code{@var{H}(i, j) = 0 forall i >= j+1)}.\n\ @end ifnottex\n\ \n\ The Hessenberg decomposition is usually used as the first step in an\n\ eigenvalue computation, but has other applications as well (see Golub,\n\ Nash, and Van Loan, IEEE Transactions on Automatic Control, 1979).\n\ @end deftypefn") | |
| DEFUN_DLD | ( | hess | , | |
| args | , | |||
| nargout | ||||
| ) |
Definition at line 38 of file hess.cc.
References arg(), octave_value::columns(), octave_value::complex_matrix_value(), empty_arg(), error_state, octave_value::float_complex_matrix_value(), octave_value::float_matrix_value(), gripe_square_matrix_required(), gripe_wrong_type_arg(), ComplexHESS::hess_matrix(), HESS::hess_matrix(), FloatComplexHESS::hess_matrix(), FloatHESS::hess_matrix(), octave_value::is_complex_type(), octave_value::is_real_type(), octave_value::is_single_type(), octave_value::matrix_value(), print_usage(), octave_value::rows(), ComplexHESS::unitary_hess_matrix(), HESS::unitary_hess_matrix(), FloatComplexHESS::unitary_hess_matrix(), and FloatHESS::unitary_hess_matrix().
 1.7.1
1.7.1