#include <stdlib.h>#include "lo-math.h"#include "lo-ieee.h"#include "oct.h"#include "parse.h"#include "ov-fcn-handle.h"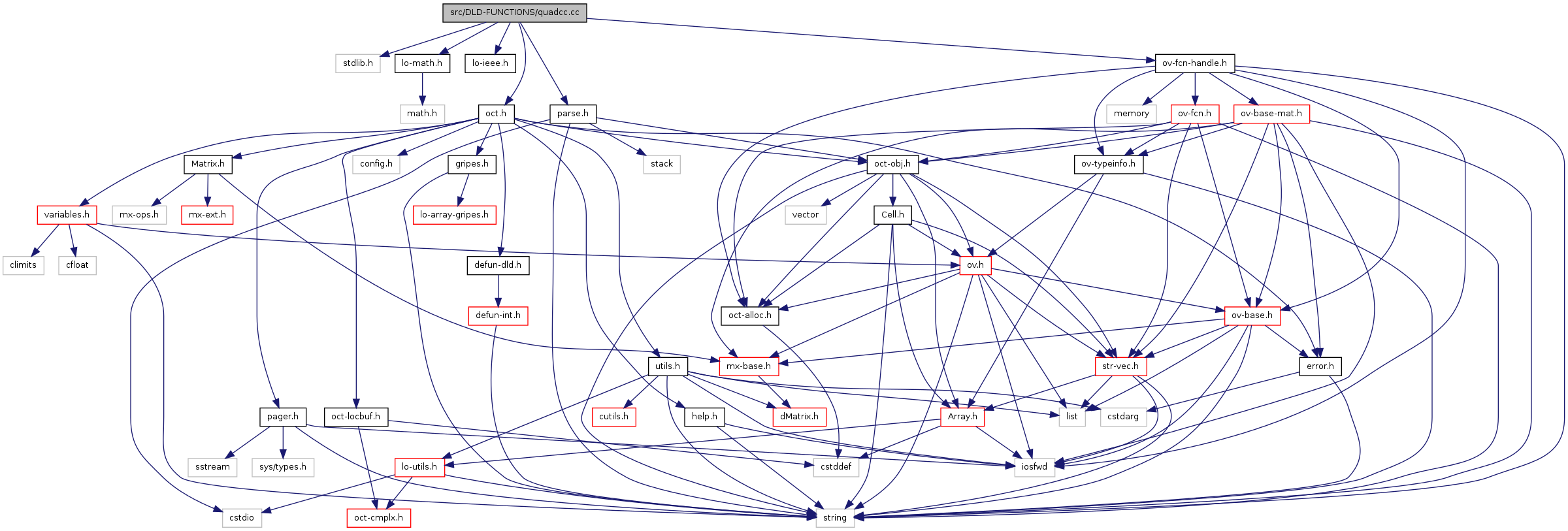
Go to the source code of this file.
Classes | |
| struct | cquad_ival |
Defines | |
| #define | cquad_heapsize 200 |
Functions | |
| DEFUN_DLD (quadcc, args, nargout,"-*- texinfo -*-\n\ @deftypefn {Function File} {@var{q} =} quadcc (@var{f}, @var{a}, @var{b})\n\ @deftypefnx {Function File} {@var{q} =} quadcc (@var{f}, @var{a}, @var{b}, @var{tol})\n\ @deftypefnx {Function File} {@var{q} =} quadcc (@var{f}, @var{a}, @var{b}, @var{tol}, @var{sing})\n\ @deftypefnx {Function File} {[@var{q}, @var{err}, @var{nr_points}] =} quadcc (@dots{})\n\ Numerically evaluate the integral of @var{f} from @var{a} to @var{b}\n\ using the doubly-adaptive Clenshaw-Curtis quadrature described by P. Gonnet\n\ in @cite{Increasing the Reliability of Adaptive Quadrature Using Explicit\n\ Interpolants}.\n\ @var{f} is a function handle, inline function, or string\n\ containing the name of the function to evaluate.\n\ The function @var{f} must be vectorized and must return a vector of output\n\ values if given a vector of input values. For example,\n\ \n\ @example\n\ f = @@(x) x .* sin (1./x) .* sqrt (abs (1 - x));\n\ @end example\n\ \n\ @noindent\n\ which uses the element-by-element `dot' form for all operators.\n\ \n\ @var{a} and @var{b} are the lower and upper limits of integration. Either\n\ or both limits may be infinite. @code{quadcc} handles an inifinite limit\n\ by substituting the variable of integration with @code{x=tan(pi/2*u)}.\n\ \n\ The optional argument @var{tol} defines the relative tolerance used to stop\n\ the integration procedure. The default value is @math{1e^{-6}}.\n\ \n\ The optional argument @var{sing} contains a list of points where the\n\ integrand has known singularities, or discontinuities\n\ in any of its derivatives, inside the integration interval.\n\ For the example above, which has a discontinuity at x=1, the call to\n\ @code{quadcc} would be as follows\n\ \n\ @example\n\ int = quadcc (f, a, b, 1.0e-6, [ 1 ]);\n\ @end example\n\ \n\ The result of the integration is returned in @var{q}.\n\ @var{err} is an estimate of the absolute integration error and\n\ @var{nr_points} is the number of points at which the integrand was evaluated.\n\ If the adaptive integration did not converge, the value of\n\ @var{err} will be larger than the requested tolerance. Therefore, it is\n\ recommended to verify this value for difficult integrands.\n\ \n\ @code{quadcc} is capable of dealing with non-numeric\n\ values of the integrand such as @code{NaN} or @code{Inf}.\n\ If the integral diverges, and @code{quadcc} detects this,\n\ then a warning is issued and @code{Inf} or @code{-Inf} is returned.\n\ \n\ Note: @code{quadcc} is a general purpose quadrature algorithm\n\ and, as such, may be less efficient for a smooth or otherwise\n\ well-behaved integrand than other methods such as @code{quadgk}.\n\ \n\ The algorithm uses Clenshaw-Curtis quadrature rules of increasing\n\ degree in each interval and bisects the interval if either the\n\ function does not appear to be smooth or a rule of maximum\n\ degree has been reached. The error estimate is computed from the\n\ L2-norm of the difference between two successive interpolations\n\ of the integrand over the nodes of the respective quadrature rules.\n\ \n\ Reference: P. Gonnet, @cite{Increasing the Reliability of Adaptive\n\ Quadrature Using Explicit Interpolants}, ACM Transactions on\n\ Mathematical Software, Vol. 37, Issue 3, Article No. 3, 2010.\n\ @seealso{quad, quadv, quadl, quadgk, trapz, dblquad, triplequad}\n\ @end deftypefn") | |
| void | downdate (double *c, int n, int d, int *nans, int nnans) |
| void | Vinvfx (const double *fx, double *c, const int d) |
Variables | |
| static const double | bee [68] |
| static const double | Lalpha [33] |
| static const double | Lgamma [33] |
| static const double | Tleft [33 *33] |
| static const double | Tright [33 *33] |
| static const double | V1inv [5 *5] |
| static const double | V2inv [9 *9] |
| static const double | V3inv [17 *17] |
| static const double | V4inv [33 *33] |
| static const double | xi [33] |
| #define cquad_heapsize 200 |
Definition at line 35 of file quadcc.cc.
Referenced by DEFUN_DLD().
| DEFUN_DLD | ( | quadcc | , | |
| args | , | |||
| nargout | ||||
| ) |
Definition at line 1472 of file quadcc.cc.
References cquad_ival::a, atan(), cquad_ival::b, cquad_ival::c, cquad_heapsize, d, cquad_ival::depth, downdate(), cquad_ival::err, error(), extract_function(), feval(), octave_base_value::function_value(), cquad_ival::fx, cquad_ival::igral, Array< T >::length(), octave_value_list::length(), M_PI, cquad_ival::ndiv, octave_Inf, octave_NaN, print_usage(), cquad_ival::rdepth, unique_symbol_name(), Vinvfx(), warning(), xfinite(), and xisinf().
Definition at line 1441 of file quadcc.cc.
Referenced by DEFUN_DLD().
Definition at line 1393 of file quadcc.cc.
Referenced by DEFUN_DLD().
{
0.00000000000000e+00, 2.28868854108532e-01, 0.00000000000000e+00,
-8.15740215243451e-01, 0.00000000000000e+00, 5.31212715259731e-01,
0.00000000000000e+00, 1.38538036812454e-02, 0.00000000000000e+00,
3.74405228908818e-02, 0.00000000000000e+00, 2.12224115039342e-01,
0.00000000000000e+00, -8.16362644507898e-01, 0.00000000000000e+00,
5.35648426691481e-01, 0.00000000000000e+00, 1.52417902753662e-03,
0.00000000000000e+00, 2.63058840550873e-03, 0.00000000000000e+00,
4.15292106318904e-03, 0.00000000000000e+00, 6.97106011119775e-03,
0.00000000000000e+00, 1.35535708431058e-02, 0.00000000000000e+00,
3.52132898424856e-02, 0.00000000000000e+00, 2.06946714741884e-01,
0.00000000000000e+00, -8.15674251283876e-01, 0.00000000000000e+00,
5.38841175520580e-01, 0.00000000000000e+00, 1.84909689577590e-04,
0.00000000000000e+00, 2.90936325007499e-04, 0.00000000000000e+00,
3.84877750950089e-04, 0.00000000000000e+00, 4.86436656735046e-04,
0.00000000000000e+00, 6.08688640346879e-04, 0.00000000000000e+00,
7.66732830740331e-04, 0.00000000000000e+00, 9.82753336104205e-04,
0.00000000000000e+00, 1.29359957505615e-03, 0.00000000000000e+00,
1.76616363801885e-03, 0.00000000000000e+00, 2.53323433039089e-03,
0.00000000000000e+00, 3.88872172121956e-03, 0.00000000000000e+00,
6.58635106468291e-03, 0.00000000000000e+00, 1.30326736343254e-02,
0.00000000000000e+00, 3.44353850696714e-02, 0.00000000000000e+00,
2.05025409531915e-01, 0.00000000000000e+00, -8.14985893995401e-01,
0.00000000000000e+00, 5.40679930965238e-01
}
{
5.77350269189626e-01, 5.16397779494322e-01, 5.07092552837110e-01,
5.03952630678970e-01, 5.02518907629606e-01, 5.01745206004255e-01,
5.01280411827603e-01, 5.00979432868120e-01, 5.00773395667191e-01,
5.00626174321759e-01, 5.00517330712619e-01, 5.00434593736979e-01,
5.00370233297676e-01, 5.00319182924304e-01, 5.00278009473803e-01,
5.00244319584578e-01, 5.00216403386025e-01, 5.00193012939056e-01,
5.00173220168024e-01, 5.00156323280355e-01, 5.00141783641018e-01,
5.00129182278347e-01, 5.00118189340972e-01, 5.00108542278496e-01,
5.00100030010004e-01, 5.00092481273333e-01, 5.00085755939229e-01,
5.00079738458365e-01, 5.00074332862969e-01, 5.00069458915387e-01,
5.00065049112355e-01, 5.00061046334395e-01, 5.00057401986298e-01
}
{
0.0, 0.0, 5.16397779494322e-01, 5.07092552837110e-01, 5.03952630678970e-01,
5.02518907629606e-01, 5.01745206004255e-01, 5.01280411827603e-01,
5.00979432868120e-01, 5.00773395667191e-01, 5.00626174321759e-01,
5.00517330712619e-01, 5.00434593736979e-01, 5.00370233297676e-01,
5.00319182924304e-01, 5.00278009473803e-01, 5.00244319584578e-01,
5.00216403386025e-01, 5.00193012939056e-01, 5.00173220168024e-01,
5.00156323280355e-01, 5.00141783641018e-01, 5.00129182278347e-01,
5.00118189340972e-01, 5.00108542278496e-01, 5.00100030010003e-01,
5.00092481273333e-01, 5.00085755939229e-01, 5.00079738458365e-01,
5.00074332862969e-01, 5.00069458915387e-01, 5.00065049112355e-01,
5.00061046334395e-01
}
{
.47140452079103168293e-1, .37712361663282534635, .56568542494923801952,
.37712361663282534635, .47140452079103168293e-1,
-.81649658092772603273e-1, -.46188021535170061160, 0,
.46188021535170061160, .81649658092772603273e-1, .15058465048420853962,
.12046772038736683169, -.54210474174315074262, .12046772038736683169,
.15058465048420853962, -.21380899352993950775, .30237157840738178177, -0.,
-.30237157840738178177, .21380899352993950775, .10774960475223581324,
-.21549920950447162648, .21549920950447162648, -.21549920950447162648,
.10774960475223581324
}
{
-1., -0.99518472667219688624, -0.98078528040323044912,
-0.95694033573220886493, -0.92387953251128675612,
-0.88192126434835502970, -0.83146961230254523708,
-0.77301045336273696082, -0.70710678118654752440,
-0.63439328416364549822, -0.55557023301960222475,
-0.47139673682599764857, -0.38268343236508977173,
-0.29028467725446236764, -0.19509032201612826785,
-0.098017140329560601995, 0., 0.098017140329560601995,
0.19509032201612826785, 0.29028467725446236764, 0.38268343236508977173,
0.47139673682599764857, 0.55557023301960222475, 0.63439328416364549822,
0.70710678118654752440, 0.77301045336273696082, 0.83146961230254523708,
0.88192126434835502970, 0.92387953251128675612, 0.95694033573220886493,
0.98078528040323044912, 0.99518472667219688624, 1.
}
Definition at line 50 of file quadcc.cc.
Referenced by DEFUN_DLD().
 1.7.1
1.7.1